3층 신경망의 구조

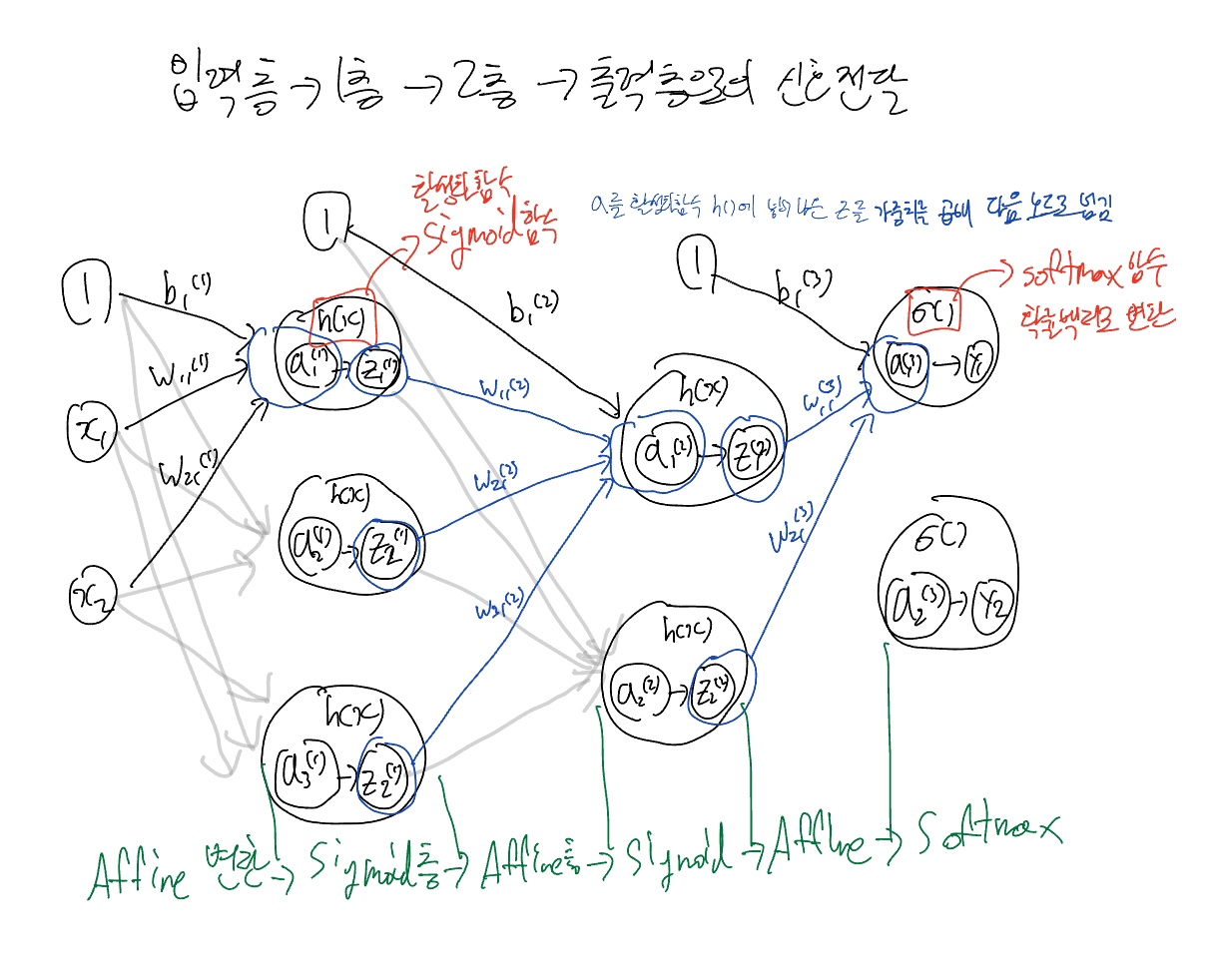
먼저 3층 신경망은 입력층(0층), 1층, 2층, 3층(출력층)과 같이 이루어져 있다.
신호 전달 과정을 살펴보자면
- 각각의 값에 가중치를 곱해 편향과 함께 더한 후(soma의 역할) 다음 노드로 넘겨준다.
- 그 안에서 h(x)라는 sigmoid함수를 통해 다음 층으로 넘길 값을 정한다.
- 그 과정을 노드의 개수만큼 실행한 후 각 노드에서 나온 값에 가중치를 곱한 후 편향과 함께 더해주고 다음 층으로 넘겨준다.
- 마지막 3층에서는 softmax함수를 통해 벡터를 확률벡터로 변환을 하여 출력한다.
- 각각의 함수는 용도에 따라 지정이 가능하다.
행렬
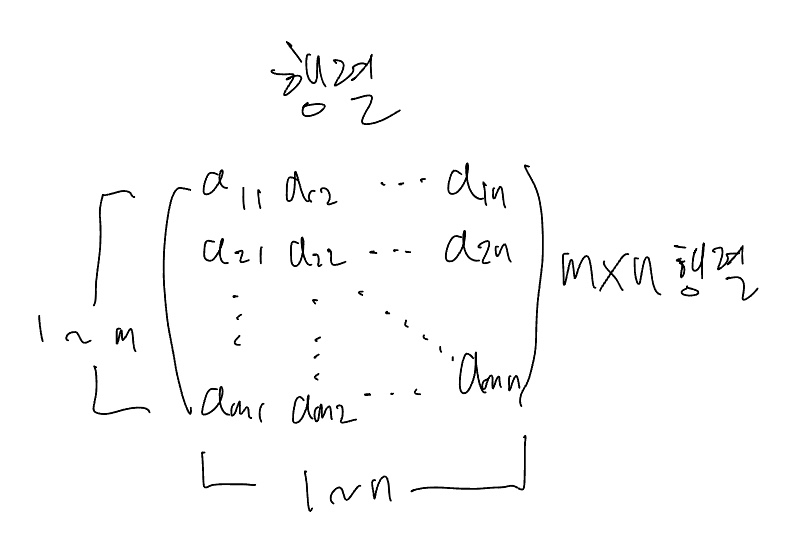
행렬은 수학에서 기본이면서도 중요한 부분이다.
가로줄을 행(row), 세로줄을 열(column)이라고 하는데 가령 가로줄이 3줄, 세로줄이 2줄이라고 하면 (3, 2) 형태의 행렬이라고 한다. 이 행렬의 두번째 가로줄에 첫번째 세로줄에 있는 값을 찾고싶을땐, A(21)과 같이 표기하면 된다.
각각의 값들을 원소라고 한다. 코드로 구현할 때 파이썬의 인덱스 규칙에 의해 0번째부터 시작하기 때문에 (2, 1)을 찾고싶을 땐 하나씩 뺀 값인 (1, 0)을 입력하면 원하는 값이 나온다.
import numpy as np
A = np.array([[1, 2], [3, 4], [5, 6]])
A, A[1][0], A.shape(array([[1, 2],
[3, 4],
[5, 6]]),
3,
(3, 2))행렬의 연산
행렬의 사칙연산은 굉장히 효울적이다. 만약 행렬 A * 2를 한다면 각각의 원소에 2를 곱하는 형태이다. 합도 마찬가지인데 각각의 원소에 원하는 값을 하나씩 더해주는 구조이다.
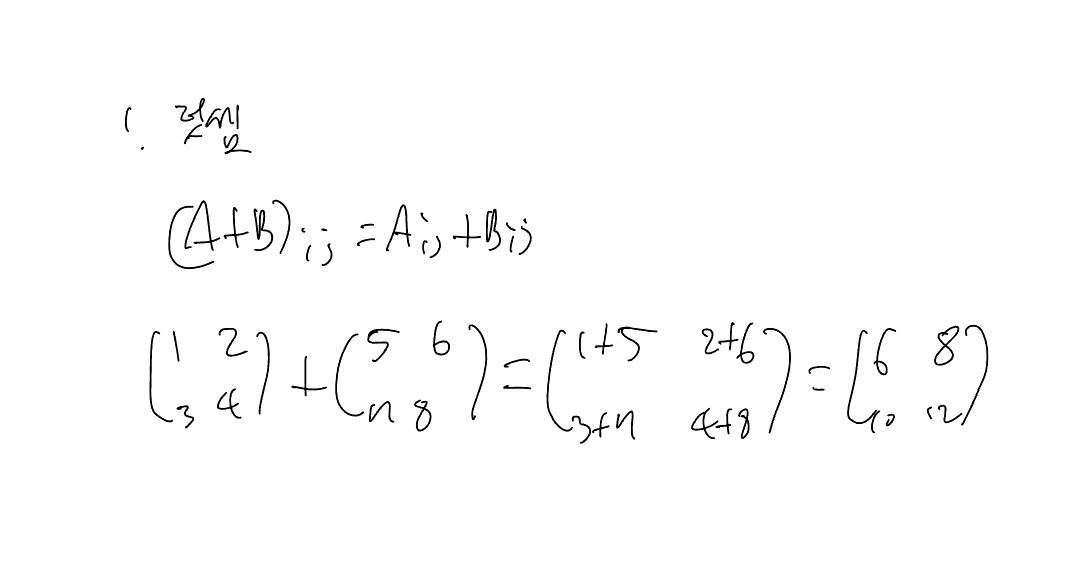
import numpy as np
A = np.array([[1, 2], [3, 4], [5, 6]])
A + 3array([[4, 5],
[6, 7],
[8, 9]])
import numpy as np
A = np.array([[1, 2], [3, 4], [5, 6]])
A * 2array([[ 2, 4],
[ 6, 8],
[10, 12]])
행렬의 연산 - 아다마르 곱셈 (Hadamard product)
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
A, B, A * B(array([[1, 2],
[3, 4]]),
array([[5, 6],
[7, 8]]),
array([[ 5, 12],
[21, 32]]))
이러한 방식의 행렬 곱셈을 아다마르 곱셈이라고 부른다. 위치에 맞는 값을 상수배 하듯이 곱해준다. 딥러닝에서는 이 곱셈을 자주 사용한다.
행렬의 연산 - 행렬 곱셈 (Dot product)

하지만 행렬과 행렬의 곱은 경우가 다르다. m x n행렬과 n x l행렬의 곱은 m x l 행렬이다.
예를들어 2 X 3행렬과 3 X 2행렬을 곱하면 2 X 2행렬이 된다. 이 때 앞 행렬의 열 값과 뒤 행렬의 행 값이 동일해야 곱셈이 가능하다. 또한 행렬의 곱은 교환법칙이 성립하지 않는다.
위의 예시를 보면 알 수 있는데 (3, 3) x (3, 2) 행렬의 앞뒤를 바꿔보면 (3, 2) x (3, 3)이 되는데 2와 3은 다르기 때문에 곱셈이 불가하다.
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
B = np.array([[1, 2], [3, 4], [5, 6]])
print(np.dot(A,B)) # (3, 3) x (3, 2)
np.matmul(B, A) # (3, 2) x (3, 3)[[ 22 28]
[ 49 64]
[ 76 100]]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-> in <cell line: 6>()
4 B = np.array([[1, 2], [3, 4], [5, 6]])
5 print(np.dot(A,B)) # (3, 3) x (3, 2)
----> 6 np.matmul(B, A) # (3, 2) x (3, 3)
ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 3 is different from 2)위의 예시를 보면 알 수 있듯이 shape에 따라 결과가 나오기도, 오류가 뜨기도 한다.
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[1, 2], [3, 4], [5, 6]])
A, B, np.dot(A,B), np.matmul(B, A)(array([[1, 2, 3],
[4, 5, 6]]),
array([[1, 2],
[3, 4],
[5, 6]]),
array([[22, 28],
[49, 64]]),
array([[ 9, 12, 15],
[19, 26, 33],
[29, 40, 51]]))행렬의 곱을 코드로 구현하려면 numpy의 함수인 np.dot(A, B) 또는 np.matmul(A, B)를 사용하면 된다.
두 행렬은 각각 (2, 3), (3, 2)의 shape로 자리를 바꿔도 값은 다르지만 각각의 결과값이 나오는 것을 볼 수 있다.
행렬 - Transposition
Transposition : 대각을 기준으로 뒤집는다.

A, A.T # A와 A의 전치행렬(array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]),
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]]))B, B.T # B와 B의 전치행렬(array([[1, 2],
[3, 4],
[5, 6]]),
array([[1, 3, 5],
[2, 4, 6]]))인공신경망의 작동 방식을 행렬로 표현하기

w의 입력과 출력은 들어가기 전 노드의 순서와 들어갈 노드의 순서이다. 예를 들면 세번째 노드에서 두번째 노드로 들어갈 때 w의 입력과 출력은 3, 2가 된다.
식의 형태로 작성한 부분과 행렬 형태로 작성한 부분의 결과는 같다.
결국 풀어서 작성한 스칼라 형태의 값과 행렬 계산을 통해 찾은 값이 같지만 파이썬으로 구현할 때 numpy가 벡터, 행렬, tensor에 특화된 라이브러리라서 훨씬 빠르다.
파이썬으로 구현해보면
import numpy as np
def sigmoid(x): # 시그모이드 함수
return 1 / (1 + np.exp(-x))
def identity_function(x): # 항등함수
return x
def init_network(): # 초기 신경망 정의
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x): # 순전파
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5]) # x1, x2
y = forward(network, x)
print(y)[0.31682708 0.69627909]
코드에서 아직 softmax를 구현하지 않았지만 이런 방식으로 신호를 전달하는 것을 볼 수 있다.
Softmax 변환
확률벡터
확률벡터는 확률을 벡터 형태로 만든 것이다. 각각의 확률은 항상 0 이상이고 모든 확률값을 더하면 항상 1이다.

Softmax 변환

일반적인 벡터가 주어져 있을 때 exp(x)를 적용하여 지수함수로 바꾸어 모든 값을 0 이상으로 바꾼다. 그 후 모든 값을 다 더한 값을 분모로 이용하여 각각의 값에 적용하면 총합이 1인 확률벡터로 바뀐다. softmax의 중요한 특징은 입력벡터 (a1, a2, ..., an)과 (a1 + C, a2 + C, ..., an + C)의 softmax값은 동일하다. 이를 이용해 overflow를 방지할 수 있다.
- overflow : 메모리에 숫자를 저장하는데 숫자가 굉장히 크면 한정된 메모리 안에 저장할 수 없어서 처리를 못한다. 개념적으로는 무한대가 아니지만 무한대로 인식하게 된다.
import numpy as np
a = np.array([1010, 1000, 990])
np.exp(a) / np.sum(np.exp(a)) # overflow된 상황<ipython-input-:5: RuntimeWarning: overflow encountered in exp
np.exp(a) / np.sum(np.exp(a))
<ipython-input-5: RuntimeWarning: invalid value encountered in divide
np.exp(a) / np.sum(np.exp(a))
array([nan, nan, nan])
보다시피 overflow로 인해 오류가 난 것을 확인할 수 있다. 이럴 땐 최댓값을 빼 계산하는 방법이 있다. 앞서 말한 softmax의 중요한 특징을 이용하면 된다.
c = np.max(a)
a - carray([ 0, -10, -20])
값이 전보다 많이 작아졌다.
np.exp(c - a) / np.sum(np.exp(c - a))array([2.06106005e-09, 4.53978686e-05, 9.99954600e-01])
이렇게 전과는 달리 잘 출력된 것을 볼 수 있다.

직접 풀어보면 결국 상수값을 더하더라도 결과가 같다는 것을 알 수 있다.
# softmax 코드
def softmax(x):
if x.ndim == 2: # 여긴 나중에 배울것임
x = x.T
x = x - np.max(x, axis = 0)
y = np.exp(x) / np.sum(np.exp(x), axis = 0)
return y.T
x = x - np.max(x) # 오버플로 대책
return np.exp(x) / np.sum(np.exp(x))- tensor는 3차원이다. 스칼라는 0차원 텐서, 벡터는 1차원 텐서, 행렬은 2차원 텐서이다.
★ ★ ★ ★ ★
이 블로그는 수익창출을 목적으로 하지 않고, 제가 공부를 하기 위해 운영하고 있습니다.
따라서, 블로그 내의 모든 콘텐츠는 제 주관적인 의견과 경험을 바탕으로 작성되었으며, 모든 정보의 정확성을 보장할 수 없습니다.
만약 블로그 내의 정보에 대해 의문이 있으시거나, 정확하지 않은 정보를 발견하신다면, 언제든지 저에게 알려주시기 바랍니다.
이 블로그가 여러분의 공부에 도움이 되기를 바랍니다.
감사합니다.
★ ★ ★ ★ ★
참고한 강의 : 수원대학교 데이터과학부 한경훈 교수님의 딥러닝 1 강의
https://www.youtube.com/playlist?list=PLBiQZMT3oSxW1RS1hn2jWBgswh0nlcgQZ
'2024 Study Plan > 머신러닝&딥러닝' 카테고리의 다른 글
| 3 (1) | 2025.01.21 |
|---|---|
| 2 (0) | 2025.01.21 |
| 1 (1) | 2025.01.17 |
| [딥러닝1] 2강. 활성화 함수 (1) | 2024.07.23 |
| [딥러닝1] 1강. 퍼셉트론 (1) | 2024.07.18 |

